here two methods are shown, whereby the last one is the only reliable one
in terms of efficiency.
- [1] Monte-Carlo-Method
- [2] The integral table method
- Histograms
- Using an envelope as a distribution function
- Example of granular synthesis with drawing random distributions
- Server side random distribution
interesting links related to random distribution:
[1] Monte-Carlo-Method:
The area of the function is used to specify whether a random x-y-pair falls below or above (Monte-Carlo-Method)The distribution acts as a limit function and find values that meet this constraint.
The disadvantage is that the efficiency of this method might vary inexpectedly and even fail.
(
g = { arg irpow=0.6, size=100;
var x, y, a, min, max;
a = Array.fill(size, { arg i; abs(i)**((1 / irpow) - 1) }).normalizeSum;
min = a.minItem;
max = a.maxItem;
a = a.collect { |el| el.linlin(min, max, 0, 1) };
while {
y = 1.0.rand;
x = a.blendAt(size.asFloat.rand);
//x.postln;
x < y
};
x
};
)
g.value;
[2] Using an integrated function table
(why this works: see here)
(
f = {arg irpow=0.9, size=100;
var a, b, sum=0;
a = Array.fill(size, { arg i; abs(i)**((1 / irpow) - 1) });
size = a.size;
a = a.collect { |el| sum = sum + el }; // incrementally integrate
a = a.normalize(0, size-1); // divide by sum (maximum value) and scale by max index
b = Array.fill(size, { arg i; a.indexInBetween(i) }); // flip array
b = b / size // rescale to 0..1
}
)
z = f.value(0.9, 200);
z.plot;
// now this produces values of the desired distribution:
z.blendAt((z.size - 1).asFloat.rand);
Using a histogram, one can test if the results are appropriate:
(
var randomNumbers, histogram, maxValue = 500.0, numVals = 100000, f, z, dfunc, size=200;
//dfunc = { arg i; var pow=0.056; i = i / size; abs(i)**((1 / pow) - 1) };
dfunc = { arg i; i = i / size; (sin(i * 80) * 0.3 + sin(i * 23)).max(0) };
f = { arg func, size = 100;
var a, b, sum=0;
a = Array.fill( size, func );
a = a.collect { |el| sum = sum + el }; // incrementally integrate
a = a.normalize(0, size-1); // divide by sum (maximum value) and scale by max index
b = Array.fill(size, { arg i; a.indexInBetween(i) }); // flip array
b = b / size // rescale to 0..1
};
z = f.value( dfunc, size );
// plot a sample of the underlying distribution function
Array.fill( size, { arg i; dfunc.value( i )}).plot("distribution function");
// now this produces values of the desired distribution:
randomNumbers = Array.fill(numVals, { z.blendAt((z.size.asFloat - 1).rand); }) * maxValue;
z.plot("mapping table");
histogram = Signal.newClear(maxValue);
randomNumbers.do({ arg each; var count, histoIndex;
histoIndex = each.asInteger;
count = histogram.at(histoIndex);
histogram.put(histoIndex, count + 1)
});
histogram.plot("histogram for distribution function application 0 - " ++ maxValue);
)
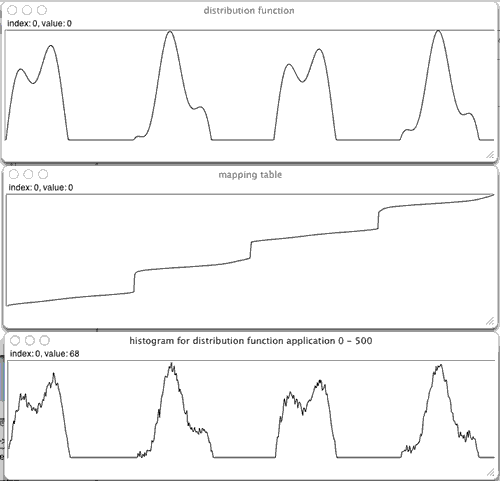
For the function:
dfunc = { arg i; i = i / size; (sin(i * 80) * 0.3 + sin(i * 23)).max(0) };it results in the following relation between distribution function, scaling function and histogram of the results:
Using an envelope as a distribution function:
(
var randomNumbers, histogram, maxValue = 500.0, numVals = 100000, f, z, dfunc, env, size=1500;
env = Env([0, 1, 0, 0.3, 1], [1, 1, 1, 1].normalizeSum, [-0.4,8, 'step', 'lin']).plot;
dfunc = { arg i; env[i / size] };
f = { arg func, size=100;
var a, b, sum=0;
a = Array.fill(size, func);
a = a.collect { |el| sum = sum + el }; // incrementally integrate
a = a.normalize(0, size-1); // divide by sum (maximum value) and scale by max index
b = Array.fill(size, { arg i; a.indexInBetween(i) }); // flip array
b = b / size // rescale to 0..1
};
z = f.value(dfunc, 2000);
// now this produces values of the desired distribution:
randomNumbers = Array.fill(numVals, { z.blendAt((z.size - 1).asFloat.rand); }) * maxValue;
z.plot("mapping table");
histogram = Signal.newClear(maxValue);
randomNumbers.do({ arg each; var count, histoIndex;
histoIndex = each.asInteger;
count = histogram.at(histoIndex);
histogram.put(histoIndex, count + 1)
});
histogram.plot("histogram for distribution function application 0 - " ++ maxValue);
)
Example of granular synthesis with drawing random distributions
asRandomTable and tableRand are methods part of supercollider which implement the above algorithm.
// keep z and c as a global random table
// using the "l" key (when th plot view is in focus) you can unlock the plot view and draw into the array.
// have a look at the mapping table: it changes only a very little, but this change has
// a distinct effect on the distribution
(
var v, env, size=180; // keep w, z, d global
env = Env([0, 1, 0, 0, 1, 0], [0.3, 1, 1, 1, 0.2].normalizeSum, [-0.4,8, 'step', 'lin']);
c = Array.fill(size, { arg i; env[i / size] });
z = c.asRandomTable;
// views:
v = z.plot("mapping table");
w = c.plot("distribution function");
// now this produces values of the desired distribution:
f = { z = c.asRandomTable; d.value = z; };
// dig for multislider view.
w.view.children[0].children[1].mouseUpAction = { f.value; };
)
// create a synth definition for a short grain:
(
SynthDef(\pgrain,
{ arg out = 0, freq=800, sustain=0.001, amp=0.5, pan = 0;
var window;
window = Env.sine(sustain, amp);
Out.ar(out,
Pan2.ar(
SinOsc.ar(freq),
pan
) * EnvGen.ar(window, doneAction:2)
)
}
).store;
)
// play a task definition. Tdef(\x).play;
// this definition can be changed on the fly :
(
Tdef(\x, {
loop {
s.sendBundle(0.2,
["/s_new", \pgrain, -1, 1, 1, \freq, z.tableRand.linexp(0,1,200, 18000)]
);
0.03.wait;
}
});
)
Server side random distribution
// tuning randomness on the server with the above created randomTable
// using waveshaping, the same method can be done on an audio signal:
// allocate a buffer and write the random table into them
s.sendBundle(nil, ["/b_alloc", 144, 1, z.size, ["/b_setn", 144, 0, z.size] ++ z]);
// play a placeholder proxy
Ndef(\x).play;
// use the random values for sine frequency distribution
(
Ndef(\x, {
var inRand, outRand;
inRand = TRand.kr(0, 1.0, Impulse.kr(MouseY.kr(0.2, 400, 1)));
outRand = Shaper.kr(144, inRand);
SinOsc.ar(
LinExp.kr(outRand, 0, 1, 300, 7000)
) * 0.1
});
)
// or for colored noise:
(
Ndef(\x, {
var inRand, outRand;
inRand = WhiteNoise.ar;
outRand = Shaper.ar(144, inRand);
})
)
// to continue editing the distribution with the GUI left from above, use this function:
(
f = {
z = c.asRandomTable;
d.value = z;
s.sendBundle(nil, ["/b_setn", 144, 1, z.size] ++ z);
};
)
// end, clear variables
d = z = w = nil;
Ndef(\x).clear;
Tdef(\x).clear;
- more on interactive programmming with sc
- download code file: arbritrary_distribution_granular_example.rtf
